Lógica modal proposicional e a semântica de mundos possíveis (5)

Em meu último texto da série sobre lógica, falei sobre a lógica de predicados de primeira ordem, o que envolve o que foi abordado anteriormente, sobre lógica proposicional, além de novos conceitos. Vimos sobre predicados e seus usos na linguagem, funções proposicionais, relações entre indivíduos e suas propriedades, como a transitividade e a reflexividade; falamos sobre quantificação múltipla e algumas confusões que podem ocorrer em formalizações em que isso ocorre, além vários exemplos sobre cada tópico citado.

No presente texto, falarei sobre a lógica modal proposicional, seus conceitos principais, sua sintaxe e a semântica de mundos possíveis. Falarei sobre algumas distinções filosóficas importantes, abordarei os sistemas modais principais e mostrarei como é possível o uso da dedução natural no sistema S5, através da semântica de mundos possíveis, o que nos permitirá fazer provas de maneira mais simples e intuitiva do que no método axiomático (que é assunto para um texto futuro). Como se trata de uma introdução à lógica modal proposicional, não apresentarei de maneira sistemática o uso de quantificadores envolvendo modalidades (o que já seria lógica modal de primeira ordem). No entanto, ao final, apresentarei algumas das aplicações da lógica modal na filosofia, o que envolve  uso de quantificadores.

---

Introdução

Na Lógica Proposicional (LP), uma proposição deve ser ou verdadeira ou falsa, pelo princípio do terceiro excluído. Na Lógica Modal Proposicional (LMP) – uma extensão da lógica clássica –, isso também ocorre, mas levamos em conta não apenas estes dois valores verdade (que são os únicos possíveis), mas também o modo com que estes valores de verdade se apresentam nas proposições. Neste contexto, uma proposição pode ser possivelmente verdadeira, ou apenas contingentemente verdadeira, enquanto outra proposição pode ser impossível e outra pode ser necessariamente verdadeira.

Neste texto, apresentarei alguns conceitos da lógica modal que serão abordados em aula[1]. Na primeira e segunda seção, distinguirei alguns conceitos importantes, como as formas modais dos juízos, a distinção entre analiticidade e sinteticidade, a priori e a posteriori e os tipos de modalidade. Na terceira e última seção, apresentarei a Lógica Modal Proposicional, sua sintaxe, a semântica de mundos possíveis, a relação de acessibilidade entre mundos possíveis, os sistemas axiomáticos modais e o uso da dedução natural no sistema S5.

 

Algumas distinções importantes

Seguindo a tábua dos juízos de Kant[2], uma proposição pode ser classificada de várias formas. Quanto a sua quantidade (podendo ser universal, particular ou singular), qualidade (afirmativa, negativa ou infinita), relação (categórica, hipotética ou disjuntiva) e modalidade (problemática, assertórica ou apodítica). Dentre estas classificações, a que nos interessa é a de modalidade. Além dessa categorização, um juízo pode ser classificado em a priori ou a posteriori e analítico ou sintético.

Em relação à sua modalidade, uma proposição é dita problemática se for pensada como meramente possível, como, por exemplo, “é possível que Marte não existisse”. Neste caso, de fato, Marte existe, mas é possível que as coisas tivessem sido diferentes. São ditas assertóricas as proposições que são reais, atualmente verdadeiras, como “Marte existe”. E são apodíticas aquelas que são necessárias, isto é, que não poderiam ser nem ter sido diferentes, como “Ou Marte existe ou Marte não existe”. Chamaremos estas proposições de possível, atual e necessária, respectivamente, para evitarmos o uso da terminologia kantiana e nos aproximarmos mais do uso contemporâneo dos termos.

A distinção entre proposições analíticas e sintéticas é de caráter linguístico, e diz respeito às relações entre o significado dos termos constituintes da proposição. Uma proposição é analítica se for verdadeira em virtude dos significados dos seus constituintes, e sintética caso contrário. Dessa forma, a proposição “todo solteiro não é casado” é analítica, porque o significado da palavra “solteiro” acarreta semanticamente no predicado “não é casado”, enquanto a proposição “o Brasil é um país sul-americano” é sintética, porque sua verdade ou falsidade se dá em função dos fatos, não do significado das palavras. Vale notar que proposições analíticas são necessárias. Se o significado da palavra “solteiro” for fixado como “não casado”, então “todo solteiro não é casado” é necessariamente verdadeira. As sintéticas, por sua vez, geralmente não são necessariamente verdadeiras, mas apenas contingentemente.

Por sua vez, a distinção entre proposições a priori e a posteriori é de caráter epistêmico, isto é, diz respeito à maneira pela qual podemos verificar a verdade da proposição. Uma proposição é dita a priori se a verificação de sua verdade puder ser feita independentemente da experiência, e a posteriori caso contrário. Assim, por exemplo, “açúcar é solúvel em água” é a posteriori, porque não podemos saber se ela é verdadeira sem verificarmos experimentalmente, enquanto “x²=x.x” é a priori, porque sabemos que ela é verdadeira sem necessitar de qualquer verificação empírica.

Podemos assumir, por hora, que toda proposição analítica é a priori – já que, sendo analíticas, sua verdade depende dos significados, o que não depende da experimentação –, e que toda proposição a posteriori é sintética. Kant defendia que havia juízos sintéticos a priori, ou seja, que tinham a mesma necessidade que os juízos analíticos, mas cuja verdade não se fundamentava no significado das palavras. Há autores, como Kripke e Plantinga, que defendem que há proposições a posteriori necessárias (como “a água é H2O”), e proposições a priori contingentes (como “eu sei que 1+1=2”)[3]. Estes tópicos, porém, precisariam ser analisados com mais calma, e isso não será feito aqui. Para fins didáticos, consideraremos a coextensão entre os conceitos de necessidade e de analiticade; isto é, uma proposição será, aqui, considerada necessariamente verdadeira se e somente se for analítica.

 

Necessidade e possibilidade

Podemos falar sobre necessidade e possibilidade de várias formas diferentes. Sabemos que é impossível, por exemplo, que algo viaje mais rápido que a luz, porque as leis da física não permitem isso. No entanto, esta é uma impossibilidade física, que é mais fraca que a impossibilidade lógica. Não é logicamente impossível que algo viaje mais rápido que a luz, e é até fácil conceber algo do tipo. Por outro lado, podemos dizer que é necessário que os seres vivos se alimentem para se manterem vivos. Esta se trata de uma necessidade biológica, que é mais fraca que a física. Podemos imaginar alguma forma de vida, neste universo, que não necessite de alimentos para se manter viva. Pode-se pensar, ainda, em uma necessidade deôntica, como “Fulano deve não matar”, temporal, como “sempre será o caso que P”, epistêmica, como “é sabido que P” ou “é provado que P”, etc.

Há, portanto, diversas maneiras pelas quais podemos lidar com a necessidade e possibilidade. Para os fins deste texto, consideraremos a necessidade lógica. Assim, uma proposição é necessariamente verdadeira se e somente se sua negação for impossível, contraditória. Por outro lado, uma proposição é possivelmente verdadeira se ela não for contraditória. Assim, mesmo proposições como “há algo que viaja mais rápido que a luz”, ou “o calor sai do corpo x para o corpo y, sendo y mais quente que x”, mesmo violando leis da física, serão tomadas como possíveis, porque não são contraditórias. Proposições como “(a+b)² ≠ a²+2ab+b²” são necessariamente falsas, impossíveis, porque são contraditórias (como a aritmética básica pode ser axiomatizada, esta proposição é demonstravelmente contraditória).

 

Lógica modal proposicional (LMP)

Qualquer sistema formal completo precisa de pelo menos três componentes, a saber, uma linguagem com suas regras de bom uso (sintaxe), uma interpretação para as fórmulas desta linguagem (semântica) e uma maneira de fazer provas. Na LMP, estes três componentes são bem parecidos com a LP, sendo adicionados apenas alguns conceitos novos. É por isso, aliás, que a lógica modal, apesar de ser uma lógica não clássica, é considerada uma extensão da lógica clássica.

Sintaxe

Nosso alfabeto será composto pelos seguintes itens:

• Infinitas variáveis proposicionais (P, Q, R, …, P₁, Q₁, R₁, …)
• Operadores (∧, ∨, ↔, →, ¬, □, ◊)
• Sinais de pontuação ([, (, ), ])

E as regras de formação de fbfs (fórmulas bem formadas; expressões gramaticalmente corretas segundo a sintaxe da lógica) são dadas pela seguinte definição indutiva:

1. Qualquer variável proposicional é uma fbf
2. Se α e β são fbfs, então (α→β), (α∧β), (α∨β) e (α↔β) são fbfs.
3. Se α é uma fbf, então (¬α), (□α) e (◊α) são fbfs.
4. Nada mais é uma fbf.

Como se pode perceber, o alfabeto da LMP contém o da LP, além de mais dois operadores, a saber, o de necessidade (□) e o de possibilidade (◊). Na verdade, um deles pode ser tomado como primitivo e o outro pode ser definido em função dele. Poderíamos tomar o operador de necessidade como primitivo, por exemplo, e definir o de possibilidade como

[Def ◊]: ◊α =_df ¬□¬ α.

Ou seja, se uma proposição é possível, isso significa que sua negação não é necessária. O contrário também poderia ser feito, isto é, tomar o operador de possibilidade como primitivo e definir o de necessidade como

[Def □] □α =_df ¬◊¬ α.

Ou seja, uma proposição é necessária se não for possível que sua negação seja verdadeira. Certamente, um dos dois terá que ser tomado como primitivo, sendo passível apenas de explicação e não definição; pois, do contrário – isto é, se um fosse definido em função do outro e vice-versa –, esta seria uma definição circular.

Dessa forma, todas as fórmulas da LP também são fórmulas da LMP, porque o alfabeto da LP é um subconjunto do alfabeto da LMP. A recíproca, porém, não é verdadeira, porque há fórmulas da LMP que não são fórmulas da LP, como □(p→p), por exemplo. Da mesma forma que a sentença “a water é transparente” não é uma sentença bem formada da língua portuguesa, por ter uma palavra que não consta em seu vocabulário, a fórmula apresentada não é uma fórmula bem formada da LP porque contém um caractere que não faz parte de seu alfabeto, a saber, o operador de necessidade modal.

 

Semântica

Na Lógica Proposicional (LP), a semântica dos operadores é definida pela maneira como eles se comportam em função do valor verdade das fórmulas sobre as quais eles são aplicados. Isto é dado pela função interpretação, e pode ser mecanicamente representado através das tabelas verdade. Assim, por exemplo, sabemos que se α e β são fbfs, então (α∧β) também é uma fbf, e ela será verdadeira se e somente se tanto α quanto β forem verdadeiras. Se uma das duas ou ambas forem falsas, então (α∧β) também será falsa, e é assim que o operador de conjunção é interpretado. A conjunção, bem como todos os outros operadores da LP, é um operador verofuncional, ou seja, o valor verdade da proposição na qual ele ocorre é uma função dos valores verdade das proposições que o compõem, seguindo o princípio de composicionalidade.

Na LMP, isso se manterá para todos os operadores, com exceção dos modais, que são os novos. Ou seja, a interpretação de ∧, ∨, ↔, → e ¬ será dada por suas respectivas tabelas verdade. A novidade aqui se dá com os operadores modais □ e ◊. Diferentemente dos outros, estes operadores não são verofuncionais, ou seja, o valor de verdade da proposição na qual eles ocorrem não depende exclusivamente dos valores verdade das proposições que a compõem, mas também de outras circunstâncias que se elucidarão posteriormente.

Ao se tentar montar uma tabela verdade para esses operadores, ficamos com lugares vazios que não podem ser preenchidos, como visto abaixo

Na tabela verdade acima, a interpretação do operador de negação é totalmente definida em termos do valor verdade da fórmula α. No caso em que α é verdadeira, ¬ α é falsa, e vice-versa. Sabemos, intuitivamente, que se α é verdadeira, então ◊α também é verdadeira, porque uma proposição precisa ser possível para ser verdadeira. Isto é, da verdade de uma proposição, podemos inferir sua possibilidade. Por outro lado, se α for falsa, sabemos que □α também é falsa, porque □α só é verdadeira se α for sempre verdadeira; e, neste caso, estamos afirmando que ela é falsa.[4]

No entanto, se α for verdadeira, não podemos determinar o valor verdade de □α. Pode ser que α seja verdadeira apenas de maneira contingente, como a proposição “O Brasil é um país sul-americano”, que poderia ter sido diferente em uma outra possível realidade. E se α for falsa, não podemos determinar o valor verdade de ◊α. Pode ser que α seja falsa apenas de maneira contingente, como a proposição “O sistema solar possui apenas uma estrela”, que até agora tem se mostrada falsa, mas poderia (e pode, ainda) ter sido diferente. Não pode haver, portanto, uma tabela verdade para determinar totalmente o valor verdade de fórmulas da lógica modal proposicional, o que significa que precisamos de outra ferramenta para formalizar sua semântica.

 

Mundos possíveis

Assim como na LP, na LMP, teremos uma interpretação para as fórmulas com uma função valoração que atribuirá valores de verdade {V, F} às variáveis proposicionais que compõem a fórmula, porém, na LMP, isso será feito em cada mundo possível.

Um mundo possível é uma descrição consistente da realidade (não necessariamente da realidade atual). Isto é, é uma descrição de como as coisas poderiam ter sido caso algo tivesse sido diferente. O termo “consistente” é importante porque limita as descrições apenas àquelas que não contêm em si uma contradição, pois, nestes casos, não estaríamos falando de mundos possíveis, mas sim impossíveis.

Por exemplo, há um mundo possível em que o sistema solar não existe. Se enumerarmos os fatos deste mundo possível, não encontraremos uma contradição, uma inconsistência, e, portanto, ele é logicamente possível. Não há, porém, um mundo possível em que há uma montanha feita completamente de pedra e completamente de terra, simultaneamente, porque um estado de coisas exclui o outro. Seria contraditório afirmar que ela é composta completamente de terra e completamente de pedra ao mesmo tempo e, portanto, não há um mundo possível em que isso ocorre.

Assim, um modelo (isto é, uma interpretação) M é definido pelo trio ordenado M = ⟨W, R, V⟩, em que W é um conjunto não vazio de mundos possíveis {w₀, w₁, w₂, …}, R é uma relação binária entre os mundos de W, a saber, a relação de acessibilidade, e V é a função valoração, que atribui valores verdade às variáveis proposicionais em cada mundo de W. V(P, w) = V significa que a proposição P é verdadeira no mundo possível w.

A relação de acessibilidade é extremamente importante para a lógica modal, pois é ela que possibilita a existência de tantos sistemas, os quais permitem que tratemos de tipos diferentes de modalidade. É ela que define qual mundo possível é acessível a partir de qual mundo possível, e isso permite que trabalhemos com noções diferentes de possibilidade e necessidade, como a lógica, a temporal, a epistêmica e a deôntica, por exemplo, conforme mostrarei posteriormente.

 

Acessibilidade

A relação R de acessibilidade é uma relação diádica (isto é, uma relação entre dois indivíduos) que determina, para quaisquer dois mundos possíveis w e w’ ∈ W (sendo w e w’ distintos ou não), se a relação wRw’ se mantém ou não, isto é, se o mundo possível w’ é acessível ao mundo w ou não. Ela é definida pela seguinte equivalência: um mundo possível qualquer w’ é acessível a um mundo possível w se e somente se toda proposição verdadeira de w’ é possível em w.

Esta relação nos permite definir mais formalmente as condições de verdade para proposições possíveis e necessárias. Dessa forma, uma proposição é dita possível em w se ela for verdadeira em pelo menos um mundo possível acessível a w, e é dita necessária em w se for verdadeira em todos os mundos possíveis acessíveis a w. Formalmente,

• V(◊P, w)=V ↔ ∃w’(wRw’∧V(P, w’)=V)
• V(□P, w)=V ↔ ∀w’(wRw’→V(P, w’)=V)

Podemos pensar em um mundo possível w em que gatos não são mamíferos, mas sim anfíbios. No nosso mundo atual, não é o caso que gatos não são mamíferos, mas como no mundo w eles não são mamíferos, então a proposição “gatos não são mamíferos” é possível no nosso mundo atual, apesar de ser falsa. Ou seja, as coisas poderiam ter sido de tal maneira que no nosso mundo atual esta proposição fosse verdadeira. Poderíamos, ainda, pensar em um mundo possível w₁ em que as coisas viajam com velocidade superior à da luz. Se esse mundo for acessível ao nosso, então, como a proposição “as coisas viajam com velocidade superior à da luz” é verdadeira em w₁, ela é possivelmente verdadeira em nosso mundo atual.

No exemplo anterior, viajar com velocidade superior à da luz, ainda que seja fisicamente impossível, é logicamente e metafisicamente possível, ou seja, é algo que podemos conceber, que não é contraditório. Porém, poderíamos querer falar sobre necessidade física, de maneira que apenas os mundos possíveis que têm as mesmas leis físicas que o nosso fossem acessíveis. Nesta estrutura, a proposição “as coisas viajam com velocidade superior à da luz” seria verdadeira em um mundo possível, porque ela não é contraditória, mas esse mundo possível não seria acessível ao nosso, porque o nosso só é capaz de acessar aqueles com as mesmas leis físicas. Nesse caso, esta proposição não seria possível no nosso mundo atual, mas sim impossível, porque seria falsa em todo mundo possível acessível ao mundo atual, por mais que ela possa ser verdadeira em algum mundo possível.

O que determina a forma com que os mundos possíveis se relacionam uns com os outros, isto é, as propriedades da relação de acessibilidade, é o conjunto de axiomas que estarão presentes no sistema. Isso será melhor explicado depois.

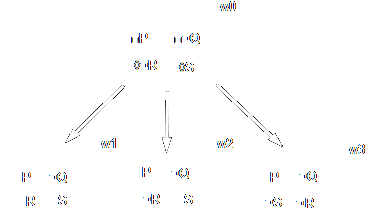
         Na estrutura acima, existem quatro mundos possíveis: w₀, w₁, w₂ e _w3, e a relação de acessibilidade entre eles, representada pela seta, é tal que w₀ acessa w₁, w₂ e w₃, e só. Ou seja, R = {⟨w₀, w₁⟩, ⟨w₀, w₂⟩, ⟨w₀, w₃⟩}. Nenhum outro mundo acessa nenhum outro mundo. Como podemos ver, P é verdadeira em todos os mundos acessíveis por w₀ e, portanto, é necessária em w₀. Q, por sua vez, é falsa em todos os mundos acessíveis por w₀, ou seja, é impossível em w₀ (o que significa que sua negação é necessária). Já S é verdadeira em pelo menos um mundo possível acessível a w₀, sendo, por isso, possível em w₀. R, por sua vez, é falsa em pelo menos um mundo possível acessível a w₀, de maneira que ¬R é possível em w₀. Nestes dois últimos casos, como ¬S e R também são verdadeiros em pelo menos um mundo possível acessível a w₀ (ainda que talvez não no mesmo), ambas também são possíveis em w₀, apesar de isso não ter sido representado.

Note que não sabemos os valores verdade de P, Q, R e S em w₀. Mesmo P sendo necessária em w₀, isso não nos permite inferir que ela é verdadeira em w₀, porque, para isso, w₀ deveria ser acessível a si mesmo, mas isso não acontece neste sistema. Isso será melhor explicado na seção seguinte.

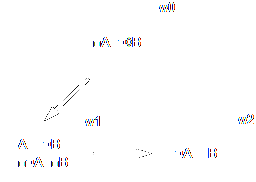
Na estrutura acima, W = {w₀, w₁, w₂} e R={⟨w₀, w₁⟩, ⟨w₁, w₂⟩}. Neste caso, A é verdadeiro em todo mundo possível acessível por w₀, e falso em w₂, que não é acessível a w₀, mas que é acessível a w1. Portanto, A é necessariamente verdadeiro em w₀ e necessariamente falso em w1. É importante perceber que aqui, novamente, um mundo possível não é acessível a si mesmo porque a seta representa a relação de acessibilidade, e um mundo possível está acessando outros mundos possíveis, mas não a si mesmo. Dessa maneira, como o mundo w₁ não é acessível a si mesmo, então mesmo A sendo verdadeiro em w₁ e falsa em 2, □¬A é verdadeiro em w₁, porque ¬A é verdadeiro em todos os mundos acessíveis a w₁.

Os exemplos anteriores fazem parte do sistema K da lógica modal (em homenagem a Saul Kripke, quem primeiro concebeu a semântica de mundos possíveis). Trata-se do sistema mais fraco, a partir do qual os demais são construídos, através de mudanças nos axiomas que constituem o sistema, o que implica em mudanças nas propriedades na relação de acessibilidade. Veremos os sistemas mais importantes da lógica modal, bem como seus axiomas característicos e sua influência nas propriedades da relação de acessibilidade.

 

Propriedades de R

A relação de acessibilidade R é uma relação entre dois indivíduos, a saber, dois mundos possíveis. Como toda relação binária, ela tem algumas propriedades, e são estas propriedades que definem a maneira com que um mundo possível pode acessar outros mundos. As principais propriedades relacionais tratadas aqui serão a reflexividade, transitividade, simetria, euclidianidade e equivalência. Há várias outras, como a funcionalidade, serialidade, direcionalidade, etc., mas que estão fora do escopo do que é proposto aqui.

Uma relação é reflexiva se um indivíduo a mantiver consigo mesmo. Por exemplo, a relação “tem o mesmo nome que” é reflexiva, porque se A tem o mesmo nome que B, então B tem o mesmo nome que A. Formalmente, se R é reflexiva, então ∀x(xRx). Dessa maneira, se a relação R de acessibilidade for reflexiva, isso significa que qualquer mundo possível w é acessível a si mesmo. Ou seja, wRw.

Uma relação é transitiva se o fato de um indivíduo x se relacionar com y e y se relacionar com z implica em x se relacionar com z. Por exemplo, a relação “é maior que” é transitiva, porque se A é maior que B e B é maior que C, então A é maior que C. Formalmente, se R é transitiva, então ∀x,y,z((xRy∧yRz)→xRz). Assim, se a relação R de acessibilidade for transitiva, isso significa que se um mundo possível w₁ é acessível a w₀ e w₂ é acessível a w₁, então w₂ é acessível a w₀. Isto é, (w₀Rw₁∧w₁Rw₂)→w₀Rw₂.

Uma relação é simétrica se a ordem dos indivíduos na relação não é relevante. Por exemplo, a relação “tem como cônjuge” é simétrica, porque A tem como cônjuge B se e somente se B tem como cônjuge A, e vice-versa. Formalmente, se R é simétrica, então ∀x,y(xRy↔yRx). Desta maneira, se a relação R de acessibilidade for simétrica, isso significa que se um mundo possível w₀ é acessível a w₁, então w₁ é acessível a w₀ e vice-versa. Isto é, w₀Rw₁↔w₁Rw₀.

Uma relação é euclidiana se o fato de um indivíduo x se relacionar com y e com z implicar em y se relacionar com z. Por exemplo, a relação “tem o mesmo nome que” é euclidiana, porque se A tem o mesmo nome que B e que C, então B tem o mesmo nome que C. Formalmente, se R é euclidiana, então ∀x,y,z(((xRy∧xRz)→yRz). Assim, se a relação R de acessibilidade for euclidiana, então se os mundos possíveis w₁ e w₂ são acessíveis a w₀, então w₁ e w₂ são acessíveis entre si.

Uma relação é de equivalência se ela for reflexiva, transitiva e simétrica. Formalmente, R é de equivalência se ∀x,y,z ((xRx)∧((xRy∧yRz)→xRz)∧(xRy↔yRx)). A relação de identidade “é idêntico a” é de equivalência, porque A=A, se A=B e B=C, então A=C, e A=B se e somente se B=A. No caso de a relação de acessibilidade R ser de equivalência, todos os mundos possíveis são acessíveis entre si.

 

Axiomas e regras de inferência

Na LMP, bem como no cálculo proposicional, também há axiomas e regras de inferências. Como a LMP é uma extensão da LP, consideraremos todos os axiomas da LP como axiomas da LP. Isso significa que todas as fórmulas da LP que são tautologias são axiomas da LMP. Além disso, é adicionado um esquema de axioma, chamado esquema de Kripke: □(α→β)→(□α→□β). Como se trata de um esquema de axioma, esta não é uma fórmula da linguagem da LMP, mas se tornará uma fórmula quando substituirmos α e β por fbfs.

As regras de inferência usadas são duas, a saber, modus ponens, que já existia na LP, e a regra da necessitação, que nos permite afirmar a necessidade de um teorema.

Modus ponens:

1. P→Q
2. P
3. ∴Q

Necessitação

1. ⊢P
2. ∴ ⊢□P

É importante perceber que a regra da necessitação diz respeito a teoremas, ou seja, ela nos diz que se nós sabemos que P é um teorema, então podemos concluir que □P também é um teorema. Esta regra não se aplica a qualquer proposição, mas sim apenas a teoremas, pois, do contrário, teríamos que “está chovendo” nos permitiria concluir que “necessariamente, está chovendo”, o que é absurdo.

O sistema mais simples que cumpre esses critérios – isto é, que tem como axiomas aqueles da lógica proposicional e os gerados a partir do esquema de Kripke, e como regras de inferência o modus ponens e a da necessitação – é o sistema K. Os axiomas deste sistema não requerem que a relação R de acessibilidade tenha alguma propriedade especial. Podemos gerar outros sistemas modais adicionando outros axiomas, que causarão mudanças nas propriedades da relação de acessibilidade.

 

Sistemas modais

K

O sistema K, como dito anteriormente, é definido pelo esquema de axioma □(α→β)→(□α→□β) e pelas regras modus ponens e necessitação. Todos os outros sistemas serão gerados a partir dele.

 

T (M)

O sistema T (também chamado M) é gerado adicionando ao sistema K o esquema de axioma □α→α. Este esquema diz que em um mundo possível, se uma fórmula é necessária, então ela é verdadeira neste mundo possível. Para provar a validade desta fórmula em T, basta negá-la e mostrar que disso segue uma contradição. Ao negar □α→α, obtém-se □α e ¬α. Se não considerarmos que a relação de acessibilidade é reflexiva, não podemos mostrar que há uma contradição, porque □α ser verdadeiro em w não nos permite inferir que α é verdadeiro em w. Assim, □α→α requer que R seja reflexiva, isto é, que todo mundo possível seja acessível a si mesmo.

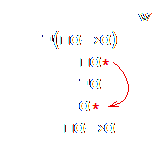
Neste caso, a contradição só pode ocorrer se a inferência mostrada pela seta vermelha seja válida, e, para isso, é necessário que a relação R, representada pela seta preta curva fora do mundo, seja reflexiva.

 

B

O sistema B é gerado ao adicionar ao sistema T o esquema de axioma α→□◊α. Este esquema diz que se uma fórmula é verdadeira, então é necessário que ela seja possivelmente verdadeira. Isto é, se ela é verdadeira em um mundo possível, então ela é possível em todos os mundos possíveis. Como o sistema B é gerado a partir do sistema T, que é reflexivo, sabemos que B também será reflexivo. Isto é, todo mundo possível é acessível a si mesmo.

Para provarmos α→□◊α em w₀, basta negá-lo e mostrar que se segue uma contradição. Negando-o, temos α e ¬□◊α, que é o mesmo que ◊¬◊α. Isso significa que há um mundo possível w₁, acessível a w₀, em que ¬◊α é verdadeiro. Em w₁, sendo ¬◊α verdadeiro, □¬α também é verdadeiro, o que significa que ¬α é verdadeiro em todo mundo possível acessível a w₀. A única maneira de derivarmos uma contradição disso é se a relação R for simétrica, isto é, se w₀ for acessível a w₁ e se w₁ for acessível a w₀. Assim, o esquema de axioma B requer que a relação R seja simétrica, conforme o diagrama abaixo.

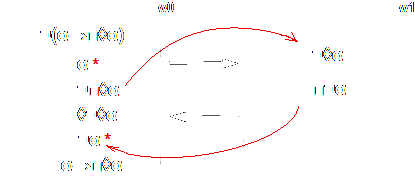
Neste caso, as setas vermelhas indicam as inferências de um mundo para o outro, e os asteriscos vermelhos indicam que há uma contradição ao se assumir a negação de α→□◊α, o que indica que esta é uma fórmula é válida, e isso só pode ocorrer se R for simétrica.

 

S4

O sistema S4 é gerado ao adicionar ao sistema T o esquema de axioma □α→□□α. Isso quer dizer que se uma fórmula é necessária em um mundo possível w, então é necessário que ela seja necessária em w. Ou seja, se uma fórmula é necessária em um mundo possível, então ela é necessária em todos os mundos possíveis.

Para provarmos que □α→□□α é verdadeira em w₀, basta assumir sua negação e derivar uma contradição. De ¬(□α→□□α) conclui-se □α e ¬□□α, que é o mesmo que ◊¬□α. Disso segue que há um mundo possível w₁, acessível a w₀, em que ¬□α é verdadeiro, e isso é o mesmo que ◊¬α. Disso se segue que há um mundo possível w₂, acessível a w₁, em que ¬α é verdadeiro, e a única maneira de derivarmos uma contradição disso é se a relação R for transitiva, porque, neste caso, □α em w₀ nos permite derivar α em w₂, que já contém ¬α. Assim, o esquema de axioma S4 corresponde à propriedade de transitividade de R, conforme o diagrama abaixo.

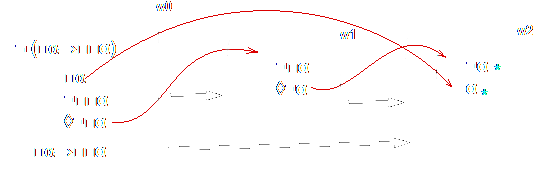
A contradição só pode ocorrer no mundo w₂ se ele for acessível a w₀, e como w₁ é acessível a w₀ e w₂ é acessível a w₁, a contradição só pode ocorrer se a relação R for transitiva, o que é representado pelas setas pretas.

 

S5

O sistema S5 é gerado ao adicionar ao sistema T o esquema de axioma ◊α→□◊α. Isso significa que se uma fórmula é possível em um mundo possível w₀, então é necessário que ela seja possível, ou seja, ela é possível em todo mundo possível acessível a w₀.

Para provar que ◊α→□◊α é verdadeiro em w, basta negá-la e derivar uma contradição. De ¬(◊α→□◊α) obtém-se ◊α e ¬□◊α, que é o mesmo que ◊¬◊α. Disso se segue que há um mundo w₁ acessível a w₀ em que ¬◊α é verdadeiro, e isso é o mesmo que □¬α. Assim, em todo mundo possível acessível a w₁, ¬α é verdadeiro. Sabemos, ainda, que em w₀, ◊α é verdadeiro, o que significa que há um mundo possível w₂ acessível a w₀ em que α é verdadeiro. A única maneira de derivar uma contradição a partir disso é se w₂ for acessível a w₁, porque, assim, α e ¬α serão verdadeiros em w₂, o que implica em a relação R ser euclidiana, conforme mostra o diagrama abaixo.

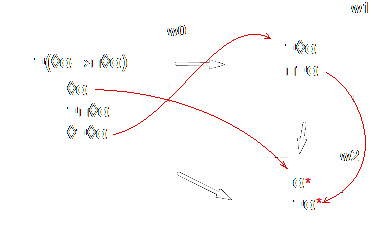
A contradição ocorre aqui porque w₀ é capaz de acessar tanto w₁ quanto w₂, e porque w₁ pode acessar w₂, o que significa que a relação R é euclidiana.

Como S5 foi gerado a partir de T, e R em T é reflexiva, R em S5 também é reflexiva. Sabemos, então, que a relação R em S5 é reflexiva e euclidiana, ou seja, xRx e (xRy∧xRz)→yRz. Suponhamos que xRy. Como R é reflexiva, temos que xRx. Temos, portanto, xRy∧xRx, o que implica em yRx, por conta da euclidianidade. Sabemos, então, que R é reflexiva, euclidiana e, agora, simétrica. Suponhamos, agora, que xRy e yRz. Por conta da simetria, temos que yRx. Então temos yRx∧yRz, o que, pela euclidianidade, implica em xRz. Se xRy e yRz implica em xRz, então R é transitiva.

Ou seja, se R é euclidiana e reflexiva, isso implica em ela ser também simétrica e transitiva, e, como vimos anteriormente, se uma relação é simétrica, transitiva e reflexiva, ela é uma relação de equivalência. Isso significa que no sistema S5, R é uma relação de equivalência; todos os mundos possíveis são acessíveis a todos os mundos possíveis.

Além disso, o sistema S5 na LMP é correto e completo, o que significa que todas e apenas as fórmulas válidas são demonstráveis. Assim como na lógica proposicional, as demonstrações das fórmulas podem ser feitas através do sistema axiomático S5, derivando todos os teoremas a partir de seus axiomas e usando modus ponens e necessitação; ou podem ser feitas través da dedução natural. Como o método axiomático é geralmente massivo e cansativo, ater-nos-emos ao método de dedução natural.

 

Dedução natural na LMP (S5)

O método de dedução natural na Lógica Modal Proposicional é bastante similar ao da lógica proposicional. Pelo teorema da dedução, qualquer fórmula válida da LP – isto é, qualquer tautologia – pode ser adicionada à prova a qualquer momento, o que significa que podemos fazer provas a partir de zero premissas. Além disso, podemos usar todas as regras de inferências normalmente usadas na dedução natural (dupla negação, silogismo disjuntivo, De Morgan, negação do condicional, etc…). Até aqui, nada de novo. O que muda é que agora teremos regras de inferência para os operadores de possibilidade e de necessidade, que antes não tínhamos.

Procederei nas provas usando o método de prova por negação, ou reductio ad absurdum, em que nós negamos aquilo que queremos provar e demonstramos que disso se segue uma contradição, o que implica que aquilo que negamos é falso – e, portanto, aquilo que queremos provar é verdadeiro. Se quisermos demonstrar que uma fórmula é válida, então, basta negá-la e mostrar que é possível derivar uma contradição em qualquer mundo possível. Se quisermos demonstrar que uma fórmula é inválida, então basta assumi-la como verdadeira e mostrar que há um contraexemplo. Como tudo que é provável em T, B e S4 também o é em S5, usarei os axiomas característicos desses sistemas como exemplos aqui, e demonstrarei sua validade.

A princípio, levemos em conta a regra da reiteração (Reit.), que nos permite fazer a interconversão entre os operadores modais:

• ¬◊α ⊢ □¬α
• ¬□α ⊢ ◊¬α

Consideremos a fórmula □P→P. Trata-se de uma instância do axioma T. Por hipótese, vamos negá-la e ver o que se segue disso.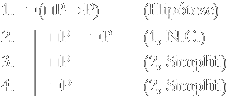

Pela regra da negação do condicional, derivamos 2 a partir de 1, e pela regra da simplificação, obtemos 3 e 4 a partir de 2. Como sabemos que o sistema S5 é reflexivo, então todo mundo possível é acessível a si mesmo. Ora, como 3 nos diz que P é necessariamente verdadeiro, então P é verdadeiro em todos os mundos possíveis acessíveis ao mundo atual, e como o mundo atual é acessível a si mesmo, segue-se que P é verdadeiro no mundo atual. Temos, então,

Como a proposição 4 contradiz a 5, concluímos, por reductio ad absurdum, que nossa hipótese inicial era falsa. Como podemos ver, utilizamos a regra de inferência “Drop Box” (ou simplesmente D.B.) para inferirmos P de □P. Sempre que tivermos uma fórmula como □α, podemos inferir α em qualquer mundo possível.

 

Consideremos, agora, a fórmula P→□◊P.

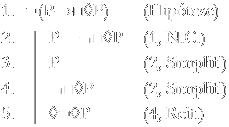
Sabemos, agora, que ¬◊P é verdadeiro em um mundo possível. Precisamos continuar a dedução para encontrarmos a contradição, e, para isso, usamos a regra “Drop Diamond” (D.D.) para abrir um novo mundo possível w₁, em que ¬◊P será verdadeiro.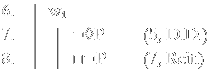

Agora que obtivemos □¬P em um mundo possível, podemos inferir ¬P em qualquer mundo possível (lembre-se de que no sistema S5, todo mundo possível é acessível a todo mundo possível). Podemos, então, voltar ao mundo anterior e inferir ¬P nele.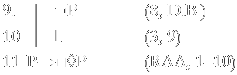

Vamos provar, agora, que □P→□□P é verdadeira. Como sabemos, esta é uma instância do esquema de axioma S4, que corresponde à propriedade de transitividade. Isso quer dizer que trabalharemos com três mundos possíveis nesta prova.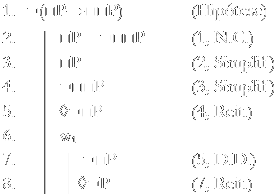

Aqui, chegamos a uma proposição possível em um mundo possível já aberto. Para prosseguirmos, nós devemos criar um outro mundo possível dentro deste já aberto.

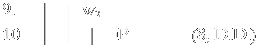
Podemos, agora, derivar a contradição, pois sabemos que □P é verdadeiro em w0, o que nos permite inferir P em qualquer mundo possível.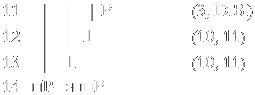

Como a proposição 10 contradiz a 11, fechamos o mundo possível w₂ e terminamos a prova, porque não pode haver uma contradição em um mundo possível.

É importante perceber que a regra D.B. foi usada em um mundo já existente. Como podemos afirmar α em qualquer mundo possível se □α for verdadeiro, poderíamos ser levados a criar já de primeira um mundo possível em que α fosse verdadeira, e, depois, usarmos a regra D.D. em ◊¬P, para fazer ¬P ser verdadeiro neste mundo e gerar a contradição. Porém, não podemos fazer isso! ◊¬P nos diz que ¬P é verdadeiro em pelo menos um mundo possível, mas não podemos saber se ele é verdadeiro especificamente naquele mundo possível que já abrimos anteriormente pela regra D.B. A estratégia é usar todas as proposições possíveis, isto é, abrir tantos mundos possíveis quanto puder, e só então usar as proposições necessárias para inferir dentro deles.

O uso destas regras é similar ao das regras de eliminação dos quantificadores universais e existenciais. A eliminação do quantificador universal pode ser feita substituindo a variável quantificada por qualquer constante individual, enquanto a eliminação do quantificador existencial só pode ser feita substituindo a variável quantificada por constantes individuais ainda não utilizadas.

Regras “Drop Box” (D.B.) e “Drop Diamond” (D.D.):

• (D.B.): □α ⊢_w α, em qualquer mundo possível w.
• (D.D.): ◊α ⊢_w α, em qualquer mundo possível w não usado anteriormente.

Para mostrarmos a invalidade de uma fórmula ou argumento, o procedimento é similar, porém, em vez de encontrarmos uma contradição, encontraremos um contraexemplo. Isto é, um conjunto de proposições em mundos possíveis que fazem as premissas verdadeiras e a conclusão falsa, no caso de um argumento, ou satisfazem as condições da fórmula, mas a tornam falsa.

 

Tomemos como exemplo (◊A∧◊B)→◊(A∧B).

Neste caso, não encontramos uma contradição. Concluímos, porém, que há dois mundos possíveis w₁ e w₂, tal que em w₁, A é verdadeiro (e, portanto, possível em w₀), B é falso e A∧B é falso; já no mundo w₂, A é falso, B é verdadeiro (e, portanto, possível em w₀), e A∧B é falso. Nesta estrutura de mundos possíveis, temos que ◊A e ◊B são verdadeiros em w₀, mas ◊(A∧B) é falso em w₀, porque A∧B é falso em todo mundo possível acessível a w₀. Encontramos, portanto, um contraexemplo, o que demonstra que a fórmula é falsa/inválida.

 

Quantificação

Como já vimos anteriormente, o uso de quantificadores se faz bastante importante ao lidar com formalizações mais complexas. Sentenças como “Todos amam alguém” podem ser formalizadas de duas maneiras logicamente diferentes, alterando a ordem com que o quantificador ocorre. Em um caso, tem-se algo como ∃x∀y(Ayx), e em outro, tem-se ∀x∃y(Axy). No entanto, uma dessas formalizações tem um significado diferente, o que não é tão visível a princípio. Enquanto ∃x∀y(Ayx) nos diz que há uma determinada pessoa tal que ela que é amada por todos, ∀x∃y(Axy) nos diz que todos amam alguém, o que não significa que todos amam a mesma pessoa.

Na lógica modal, isso também ocorre, em relação aos operadores de necessidade e possibilidade. A diferença na posição de ocorrência desses operadores pode mudar completamente o significado da frase, e geralmente é bem mais difícil perceber essa mudança, porque às vezes ela não existe na linguagem natural.

 

De re x de dicto

A sentença “se chover, necessariamente a rua molha”, pode exemplo,  pode ser formalizada como □(C⊃M), ou como C⊃□M. No primeiro caso, o operador modal ocorre antes de tudo, e seu escopo é toda a sentença condicional. Dizemos que esta ocorrência do operador é de dicto, que, no latim, significa “da proposição, da frase, do que foi dito”. Isso significa que é necessário que esta implicação seja verdadeira, ou seja, que em nenhum mundo possível possa ser o caso que C é verdadeiro e M falso. Assim, em todos os mundos possíveis é verdade que se chover, a rua molha. Isso é relativamente aceitável. Se supusermos que de fato há uma conexão causal entre chover e a rua molhar, e desconsiderarmos os mundos possíveis em que esta causalidade não ocorra ou os mundos em que alguém cobre a rua para evitar que ela molhe, então de fato é necessário que se chova, a rua molhe.

Por outro lado, em C⊃□M, temos o operador modal ocorrendo no consequente do condicional. Esta ocorrência do operador é dita de re, isto é, “da coisa”. Neste caso, a sentença nos diz apenas que se for verdade que está chovendo, então é necessário que a rua molhe. Isso é bastante estranho, porque significa que se chover agora, no mundo possível atual, então a rua molha em todos os mundos possíveis, o que é algo difícil de se aceitar.

O exemplo apresentado mostra distinção entre a ocorrência de re e de dicto do operador lógico de necessidade. Esta ocorrência pode se dar no operador de negação, também, e em outros operadores modais, como “sabe-se que”, “é obrigatório que”, etc. E, como eu disse, a história complica mais quando levamos em conta quantificadores nas fórmulas.

Se considerarmos □∀xPx e ∀x□Px, teremos, novamente, um exemplo de ocorrência de dicto e de re, respectivamente, do operador modal de necessidade. No primeiro caso, estamos afirmando que necessariamente, tudo o que existe (se assumimos um domínio de quantificação não vazio) tem a propriedade P, ou seja, em todos os mundos possíveis, qualquer indivíduo que exista é P. No segundo caso, por outro lado, afirma-se que todos os indivíduos que existem atualmente tem necessariamente a propriedade P. Ou seja, todas as coisas do nosso mundo atual tem a propriedade de ser P em todos os mundos possíveis em que elas existam. Isso significa que P é uma propriedade necessária de todas as coisas, ou seja, que não há como uma coisa não ter essa propriedade.

Curiosamente, estas duas fórmulas são logicamente equivalentes (aliás, você pode tentar demonstrar sua equivalência através da dedução natural). Isso parece implicar em os indivíduos que têm certa propriedade necessária neste mundo possível existirem em todos os mundos possíveis acessíveis ao nosso, e, como esta propriedade requer que o indivíduo exista para ser instanciada, parece que sua existência é necessária. Alguns problemas metafísicos surgem nesse âmbito, como o da identidade transmundana (Se um indivíduo a existe em dois mundos possíveis, e se estamos falando do mesmo indivíduo, então como pode ele ter certas propriedades [contingentes] em um mundo mas não tê-las no outro? Isso parece violar o princípio da indiscernibilidade dos idênticos), mas não discutirei sobre eles aqui.

 

Contextos intensionais

Sempre que nos referimos a algo, fazemos isso sempre considerando uma extensão e uma intensão. A extensão de um objeto sobre o qual falamos é o próprio objeto, por exemplo, uma determinada maçã. A intensão, por outro lado, tem a ver com a maneira pela qual nos referimos a essa determinada maçã. Por exemplo, se falarmos que a maçã que caiu sobre Isaac Newton era vermelha, estamos nos referindo a um determinado objeto, isto é, à sua extensão, porém, fazemos isso de maneira intensional, através de um sentido – a saber, o de que a maçã sobre a qual falamos é precisamente aquela que caiu no físico inglês. Um contexto é dito extensional se apenas a extensão – isto é, a denotação, a referência – daquilo sobre o qual se fala é importante para determinar a verdade da sentença, e é intensional caso a intensão – ou seja, o sentido, o modo de apresentação – seja importante para isso.

Por exemplo, a frase “maçã é uma fruta vermelha” é um contexto intensional, porque podemos determinar sua verdade apenas através da extensão do objeto (no caso, a referência da palavra ‘maçã’). Por outro lado, a frase “eu acredito que a fruta que saiu sobre Newton era vermelha” é um contexto intensional, porque a partícula ‘eu acredito que’ faz com que as condições de verdade da sentença dependam de outras coisas além da extensão daquilo sobre o qual se fala. Eu posso acreditar que maçãs são vermelhas, mas posso acreditar que foi, na verdade, uma laranja que caiu em Newton. Neste caso, a frase anterior seria falsa, porque eu teria a intensão de me referir a uma laranja com a descrição ‘a fruta que caiu sobre Newton’, e não a uma maçã. Esta diferença entre sentido e referência é importante, e precisamos considerá-la para identificarmos e evitarmos alguns problemas que ocorrem quando fazemos certas coisas em contextos intensionais.

Como mostrei no exemplo anterior, poderíamos ser levados a crer que é lícito fazer a substituição de termos idênticos em quaisquer circunstâncias. Afinal, a identidade é uma relação de equivalência e, portanto, se sabemos que A=B, podemos substituir A por B em todos os contextos nos quais A ocorre. Mas incorremos em erros quando isso é feito em contextos intensionais, e isso ocorre quando estamos lidando com modalidades.

Consideremos o seguinte argumento, exemplificado por Quine:

1. Necessariamente, 8 é igual a 8.
2. O número de planetas do sistema solar é igual a 8.
3. Portanto, necessariamente, o número de planetas do sistema solar é igual a 8

Formalizando, temos o seguinte:

1. □(8 = 8)
2. (ιx)(Px) = 8
3. ∴□((ιx)(Px) = 8)

Aparentemente o argumento é válido e as premissas são verdadeiras. De fato, se o número de planetas do sistema solar é igual a 8, então poderíamos substituir o número 8 na primeira premissa por esta descrição e chegaríamos à conclusão. Teríamos, então, uma prova de que em todos os mundos possíveis, o número de planetas do sistema solar é igual a oito. Isso, porém, é notavelmente falso. Poderia ter sido o caso que o sistema solar tivesse tido uma quantidade maior ou menor de planetas, e pode até ser que tenham mais planetas que ainda não foram descobertos, ou que haja astros que consideramos planetas mas que não sejam, etc. O ponto é que algo neste raciocínio deve estar errado, porque a conclusão é absurda.

O problema deste argumento é que apesar de os termos “8” e “o número de planetas do sistema solar” denotarem o mesmo objeto, a saber, o número 8 – ou seja, têm a mesma extensão -, estas expressões possuem sentidos diferentes, isto é, intensões diferentes. Contextos modais como este são intensionais e, portanto, não podemos fazer a substituição desses termos. Não valendo a lei da substituição dos idênticos, temos que o argumento apresentado não consegue justificar a conclusão, que não segue das premissas.

 

Conclusão

Somado ao aparato lógico que já tínhamos antes, podemos ver que as ferramentas modais abordadas aqui têm uma considerável importância na formalização de argumentos. Podemos, agora, entender a forma lógica de proposições e argumentos que se utilizem de operadores modais, como “necessariamente”, “é possível que”, “é contingente que”, etc. Vimos a existência de vários sistemas modais diferentes, apesar de não termos abordado com detalhes as aplicabilidades de cada um. Além disso, pudemos ver como a formalização de argumentos, bem como a identificação de certas propriedades dos operadores modais, nos permite identificar problemas que não seriam facilmente detectáveis com uma mera análise da linguagem natural, além de abrir espaço para questionamentos metafísicos sobre propriedades essenciais e acidentais, etc.

 

---

 

Notas

[1] Presumo, aqui, que o leitor tem conhecimento pelo menos básico de lógica proposicional e de lógica de predicados de primeira ordem.

[2] Kant, I., Crítica da Razão Pura, 2ª edição, A70/B95.

[3] Kripke, S., Naming and Necessity. Cambridge, Mass.: Harvard University Press, 1972.

[4] Importante frisar que estamos lidando aqui com uma noção bem geral de necessidade e possibilidade, sem restringi-las a um sistema específico. Como veremos, há sistemas em que a inferência α⊃◊α não é válida, por exemplo.

 

Bibliografia:

Garson, J. “Modal Logic for Philosophers”, New York, Cambridge, 2013, Second Edition.

Chihara, C. “The Worlds of Possibility – Modal Realism and Semantics of Modal Logic”, New York, Oxford University Press, 2004.

Gensler, H. “Introduction to Logic”, New York, Routledge, 2017, Third edition.

Hughes, G., Cresswell, M. “A New Introduction to Modal Logic”, London, Routledge, 1998.

Mendelsohn, R. “First Order Modal Logic”, New York, Springer Science, 1998.

McCance, Joel. “A Brief Introduction to Modal Logic”, (2008)

Mortari, C. “Introdução à Lógica”, São Paulo, Editora UNESP, 2ª edição, 2017.

Quine, W. V. O. “Reference and modality”, em “From a Logical Point of View”, Harvard University Press, Cambridge, Mass., 1953, pp. 139–159.

Tugendhat, E. “Logisch-semantische Propädeutik”, Ditzingen, Stuttgart, 1983.

Zalta, E. “Basic Concepts in Modal Logic”, Center for the Study of Language and Information, Stanford University.

---

Este texto não foi escrito no mesmo estilo que os anteriores, pois se trata de um texto que preparei como base para uma aula que apresentei. Porém, apesar de ser um pouco mais formal, acredito que os elementos didáticos se mantiveram.